How To Draw A Logarithmic Spiral

next curve

previous curve

second curves

3D curves

surfaces

fractals

polyhedra

LOGARITHMIC SPIRAL

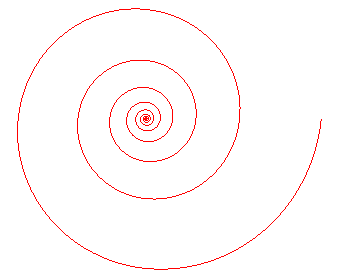
Curve studied by Descartes and Torricelli in 1638, then by Jacques Bernoulli (1654-1705).
Other names: equiangular spiral, Bernoulli spiral, spira mirabilis; the name "logarithmic spiral" was given past Varignon.

Jacques Bernoulli had a logarithmic screw engraved on its gravestone in the Basel Munster, with the epigraph: eadem mutata resurgo, "although changed (mutata), I arise (resurgo) the same (eadem)". Nevertheless, the engraver traced an Archimedean screw...

The logarithmic spiral tin can be defined every bit
    - the bend the polar tangential angle of which remains abiding (different from a correct angle)
    - the curve the curvature of which is inversely proportional to the curvilinear abscissa
    - the curve the radius of curvature of which is inversely proportional to (and greater than) the radius vector ( with l > i)
Therefore, the logarithmic spirals with centre O are the trajectories at angle. of the pencil of lines issued from O.

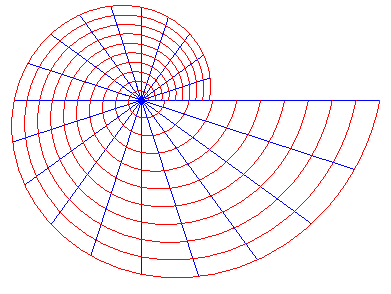
The logarithmic screw can besides have a kinematic definition every bit the trajectory of a indicate K moving on a line passing by O with a speed proportional to OM, when this line itself is in compatible rotation around O; or also as the curve in polar coordinates such that when the polar angle is in arithmetic progression, the radius vector is in geometric progression.

The logarithmic spiral is also the stereographic projection from the south pole of the rhumb lines of the spheres with centre O, forming an angle with the meridians (since the stereographic projection is a conformal map).

Finally, it is the planar expansion of an helix of a cone of revolution.

The logarithmic screw has an exceptional stability with respect to the archetype geometrical transformations:

- any rotation with centre O and bending of the spiral amounts to a homothety with aforementioned centre and ratio, which in turn amounts to the identity if. Note that the belongings "eadem mutata resurgo" is characteristic of this curve: any continuous curve which, when turned past an angle, is equal to its homothetic image with ratio(for any angle) is a logarithmic spiral with m = - ln. For an Archimedean spiral, a rotation is completely different from a homothety!

- whatsoever inversion with heart O amounts to a reflection about an axis passing past O.
- its evolute is a logarithmic spiral with aforementioned centre and same bending(and, besides, the limit of the north-thursday evolute of any curve is a logarithmic screw).

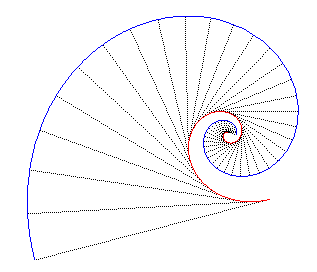
- its pedal with respect to O is a logarithmic screw with aforementioned middle and same angle.
(and do the evolutes have the same belongings?)

- its caustics by reflexion or diffraction, when the low-cal source is at O, are logarithmic spirals.

- the mating gear associated to a gear shaped similar an logarithmic screw is an isometric logarithmic screw.

When a logarithmic spiral rolls on a line, the asymptotic point describes another line:

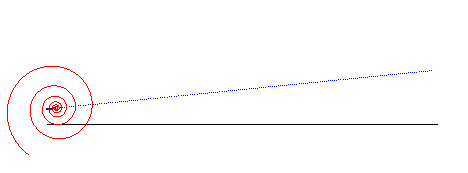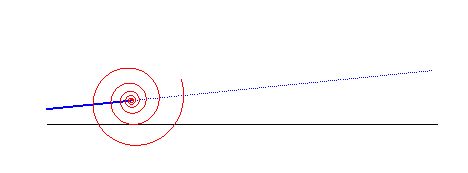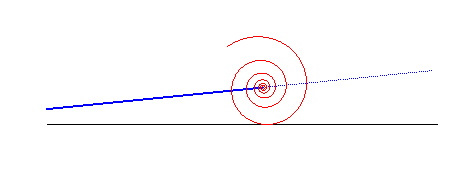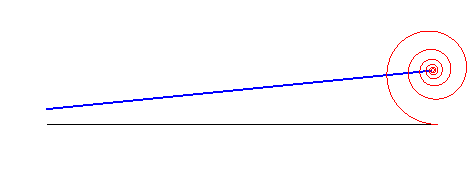
Run across some "applications" of this property at wheel-road couple.

The logarithmic spiral is a solution to the 3 following physical problems:

ane) The strength centred on O that makes a point in infinite draw a logarithmic spiral is proportional to one/r ³ (this force, according to the Binet formula, is proportional to which, here, is equal to, with u = 1/r).
2) the bend (called brachistochrone) that minimises the travel time of a point moving freely along this bend, when it is itself turning around a fixed centre O at constant speed, in the case where the speed of the moving point vanishes at O, is a logarithmic spiral.

3) A particle of mass m ₁ and charge q placed in a compatible magnetic field of intensity B with a speed v ₀ perpendicular to the field describes a logarithmic screw with and.

see: perso.libertysurf.fr/hdehaan/mecanique/M6/M6_2/M6_2_cadre.htm

If u is a complex number different from 0, so the paradigm points of the geometric sequence

with mutual ratio u are located on an exact logarithmic spiral, with parameter

.
Opposite, u = 1+i/4.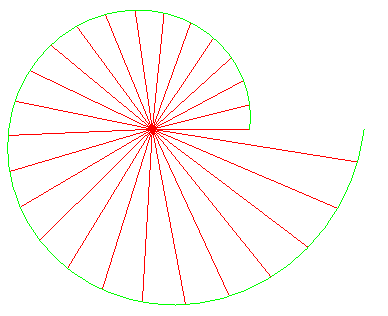

In the aforementioned way, any sequence points of polar coordinates

such that the

are in geometric progression with mutual ratio a and the

are in arithmetics progression with common difference b describes a logarithmic spiral with k = ln a / b.

For example, on the opposite figure, the points with polar coordinates ((i,i) ^thousand ; (k+twol)p/n) were traced, in blue if 50 is even, in scarlet otherwise. These points are placed in a quincunx design at the intersection betwixt concentric circles with radii in geometric progression and concurrent lines; but they are also located on the logarithmic spirals with equation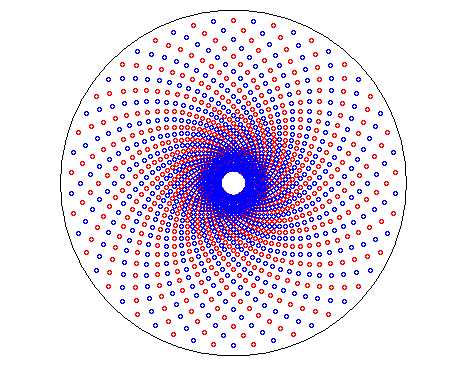, hence the overnice visual effect.

The tablecloth in my living room

View of points of polar coordinates with r = 1 005, located on the spiral, for N ranging from 0 to 100, simulating the scales. The black angle connecting the first two scales is therefore equal to the golden bending. red secondary spirals and secondary dark-green spirals appear, which rather models the sunflower florets. On the view secondary spirals. On the picture where the scales are indicated with the appearance number, we note that the k-th secondary spiral is associated with is formed of the points satisfying Northward = k + a multiple of, for k ranging from 0 to; for case, the first ruby-red spiral connects scales whose number is multiple of 21. The scales of the k-th secondary spiral associated with are located on the logarithmic spiral of polar equation where is the integer closest to, ie, seen the links between the Fibonacci sequence and the golden ratio ( is the polar bending betwixt two successive scales of a secondary spiral). Note: the angle between two blood-red and light-green spirals that intersect is constant merely non related to the gilded angle equally we sometimes see written, since it depends on the value of r!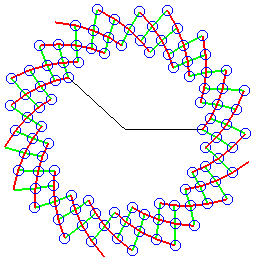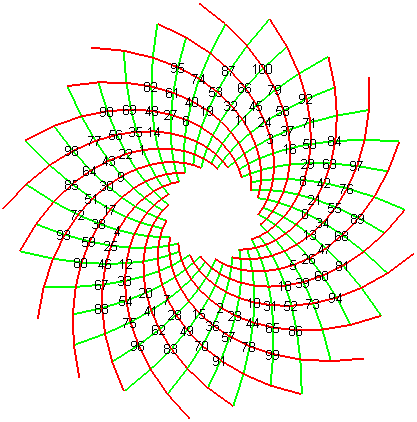
If we increase the ratio r to 1.02, it is rather the 8 = ruby spirals associated with and the 13 = green spirals associated with, which are visible naturally, equally for the pine cone; on the 2nd effigy are drawn the 34 = red spirals associated with and the 55 = light-green spirals associated with, again with r = one.005. These secondary spirals associated with the Fibonacci numbers appear visually considering multiplying the golden angle past the terms of the Fibonacci sequence yields results the moduli of which approach zero for large northward: we can run across clearly in the figure where the scales are indicated with their number of appearance that the fibonaccian scales 3, v, eight, 13, 21, 34, 55, 89 are close to the ten axis. On this page, we tin can exam different angles of rotation betwixt 2 sunflower florets and note that the arrangement of the florets is optimal in the case of the gold angle.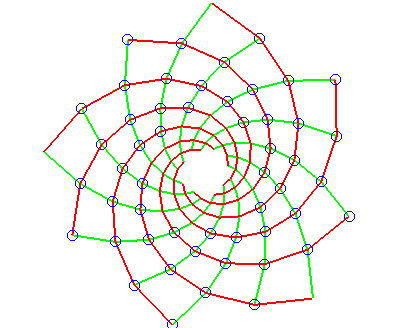

If we consider a sequence of concurrent lines D _i , D _two , .... each of them forming an angle eastward with the next one, then that if, starting from M ₁ on D ₁ , Grand ₂ on D _two is defined and then that the angle between D ₁ and M ₁ K _ii is equal to , and M ₃ , M _iv , ... are defined in the same manner, so the moduli of the points Grand _n are in geometric progression with common ratio and their arguments are in arithmetic progression with mutual difference e , and thus are on a logarithmic spiral with; information technology can be checked that goes indeed to cot as goes to 0, then that the screw corresponding togoes to the logarithmic screw with grand = cot.

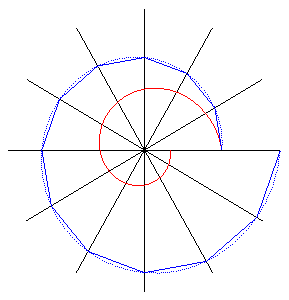here, y = 100°, e = p/x.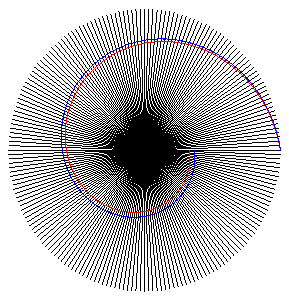

hither, y = 100°, e = p/50.

REMARK: when = xc°, 1000 _i+1 is defined so that M _i is its orthogonal projection on D _i (careful not to mistake it with the Theodore screw which is an approximate Archimedean spiral).

Another gauge construction consists in taking arcs of circles with constant angles and radii in geometric progression with common ratio, with tangential connectedness.
For a very cute special case, see the aureate spiral.
The spiral traced on a cone which is projected on a logarithmic spiral is the conical helix.